Hierarchy in wiki:
- Wiki/
- Wiki/Collision/
- Wiki/Collision/%E7%BB%BC%E8%BF%B0/%E7%A2%B0%E6%92%9E%E6%A3%80%E6%B5%8B%E6%80%BB%E7%BB%93/
细阶段
一般而言的 Narrow Phase 是基于点线面的关系推导得到的。而且在很多情况下,我们不需要知道碰撞在两个插值点之间的具体位置,而只需要知道其是否碰撞。针对不同的物体,一可以有不同的优化策略。
一般物体间的碰撞检测
- 凸物体
- 刚体
- 变形体 & 三角网格
凸物体的碰撞检测
一般而言,凸物体的碰撞可以通过 GJK 和 SAT 方法来判断。
Gilbert-Johnson-Keerthi (GJK) 算法
Idea
设 \(\mathcal A = \{\mathbf x\}\), \(\mathcal B = \{\mathbf x\}\) 是两个点集,定义其 Minkowski 差为:
不难证明,\(\mathcal A\) 和 \(\mathcal B\) 碰撞,当且仅当 $\(0 \in \mathcal A - \mathcal B\)。
问题在于,我们不可能遍历所有的点对来判断原点是否属于该集合。但是基于这样的基本思路,对于凸物体,我们可以有快速算法实现。
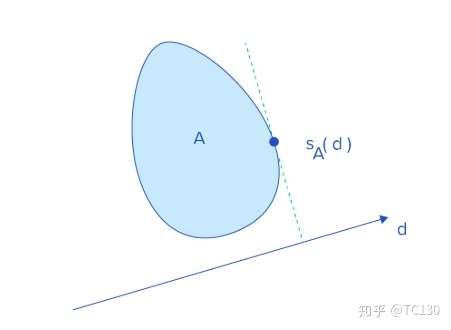
Support 函数和 Simplex 单纯形
其实我们要判断原点是否属于 Minkowski 差,就是要判断是否 Minkowski 差的一个子集包含了 \(0\),这样的操作可以在物体是凸的的时候要求其形成的单纯形。对于二维的情况,使用三角形;对于三维情况,使用四面体。
为了生成这样的单纯形,我们计算 support 函数来快速获取给定方向上的支撑点,如图所示^1。
迭代求解
有了如上的论述,我们可以通过如此构造单纯形:
- 随机生成一个单纯形
- 假定当前的单纯形为 \(\{v\}\) 则选择距离原点最远的抛弃,对于 n - 1 维单纯形求法向量,求support(两个)
- 直到
- 检查到 0 => 碰撞
- 如果新的support点,在迭代方向上的投影小于等于0 => 不碰撞
可以证明,这样的算法一定在有限步内结束。
SAT 分离轴算法
一个更朴素的思想是:(类似于SVM)两个凸集合不交,当且仅当存在一个 \(n - 1\) 维的超平面能够完全分开这两个凸集合。 遍历所有的边(三维则是面),投影到其正交补空间上。若存在一个边,能使得投影完全分离,则其是不相交的,反之相交。
刚体碰撞检测
刚体碰撞的检测正如在 Broad Phase 里提到:
凸包变换(V-HACD),并使用适用于凸包的 Collision Detect 来进行碰撞的判断。
这类方法将原来的刚体预计算处理为凸包,用户可以控制其分割的粒度,从而权衡其加速/精度。
变形体 & 三角网格
基本思路为:
- 求解三次方程;
- 设置两个非邻接顶点/面的距离下界为一个固定/可变的非零数(可以按照siggraph2022的论文结果强化到点-点距离)
- 在变形体网格上建立局部 BVH 来增加一部,返回1/2求解